
Estimating phylogenetic trees with phangorn
Klaus Schliep, Iris Bardel-Kahr
Graz University of Technology, University of Grazklaus.schliep@gmail.com
2026-02-24
Source:vignettes/Trees.Rmd
Trees.RmdIntroduction
These notes should enable the user to estimate phylogenetic trees
from alignment data with different methods using the
phangorn package (Schliep
2011) . Several functions of this package are also
described in more detail in (Paradis
2012). For more theoretical background on all the methods see
e.g. (Felsenstein 2004; Yang 2006). This
document illustrates some of the package’s features to estimate
phylogenetic trees using different reconstruction methods.
Getting started
The first thing we have to do is to read in an alignment.
Unfortunately there exist many different file formats that alignments
can be stored in. In most cases, the function read.phyDat
is used to read in an alignment. In the ape package (Paradis and Schliep 2019) and
phangorn, there are several functions to read in alignments,
depending on the format of the data set (“nexus”, “phylip”, “fasta”) and
the kind of data (amino acid, nucleotides, morphological data). The
function read.phyDat calls these other functions and
transforms them into a phyDat object. For the specific
parameter settings available look in the help files of the function
read.dna (for phylip, fasta, clustal format),
read.nexus.data for nexus files. For amino acid data
additional read.aa is called. Morphological data will be
shown later in the vignette Phylogenetic trees from morphological
data.
We start our analysis loading the phangorn package and then reading in an alignment.
library(ape)
library(phangorn)
fdir <- system.file("extdata/trees", package = "phangorn")
primates <- read.phyDat(file.path(fdir, "primates.dna"),
format = "interleaved")Distance based methods
After reading in the nucleotide alignment we can build a first tree
with distance based methods. The function dist.dna from the
ape package computes distances for many DNA substitution
models, but to use the function dist.dna, we have to
transform the data to class DNAbin. The function dist.ml
from phangorn offers the substitution models “JC69” and “F81”
for DNA, and also common substitution models for amino acids
(e.g. “WAG”, “JTT”, “LG”, “Dayhoff”, “cpREV”, “mtmam”, “mtArt”, “MtZoa”
or “mtREV24”).
After constructing a distance matrix, we reconstruct a rooted tree
with UPGMA and alternatively an unrooted tree using Neighbor Joining
(Saitou and Nei 1987; Studier and Keppler
1988). More distance methods like fastme are
available in the ape package.
We can plot the trees treeUPGMA and treeNJ
with the commands:
plot(treeUPGMA, main="UPGMA")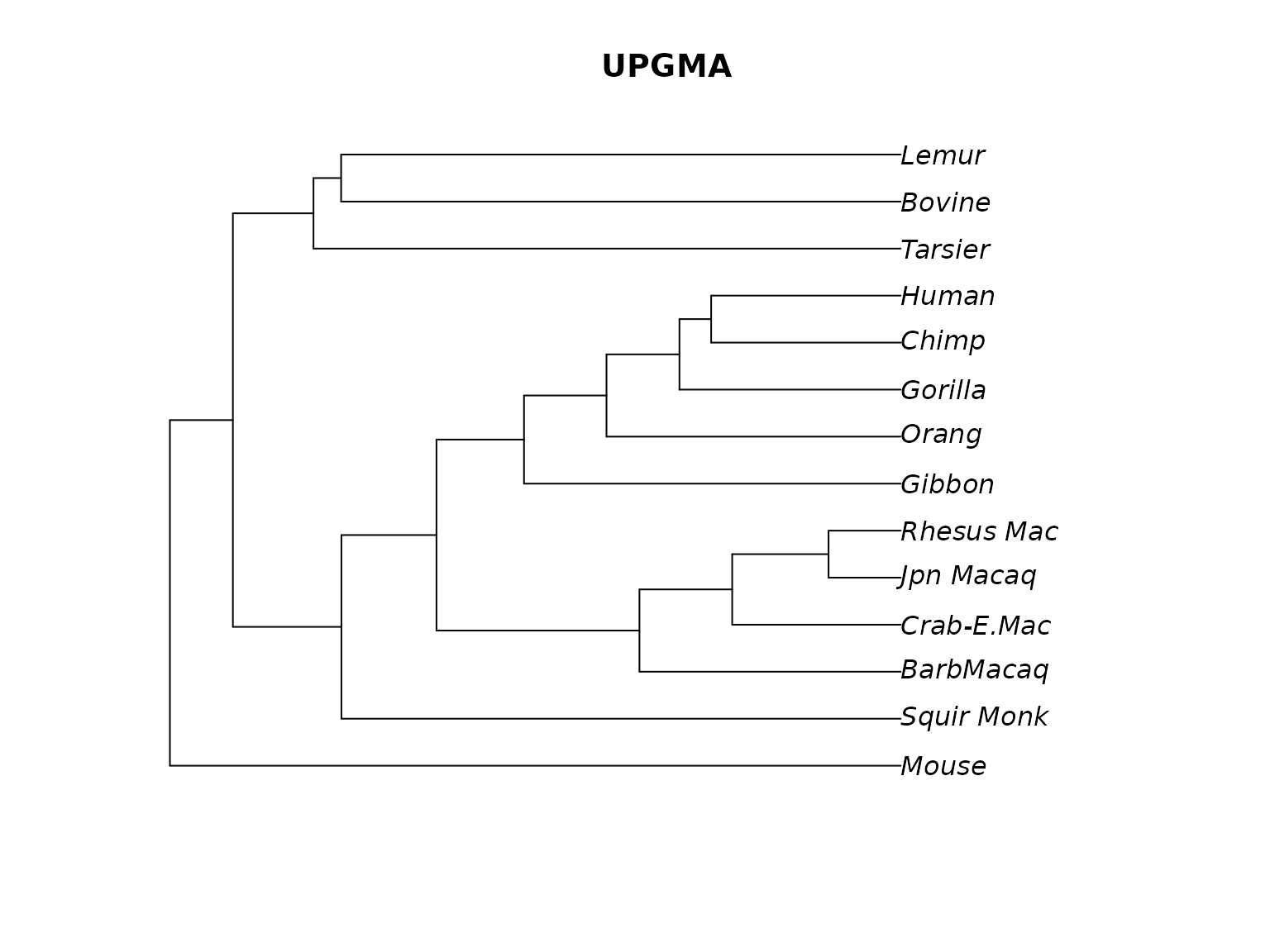
Rooted UPGMA tree.
plot(treeNJ, "unrooted", main="NJ")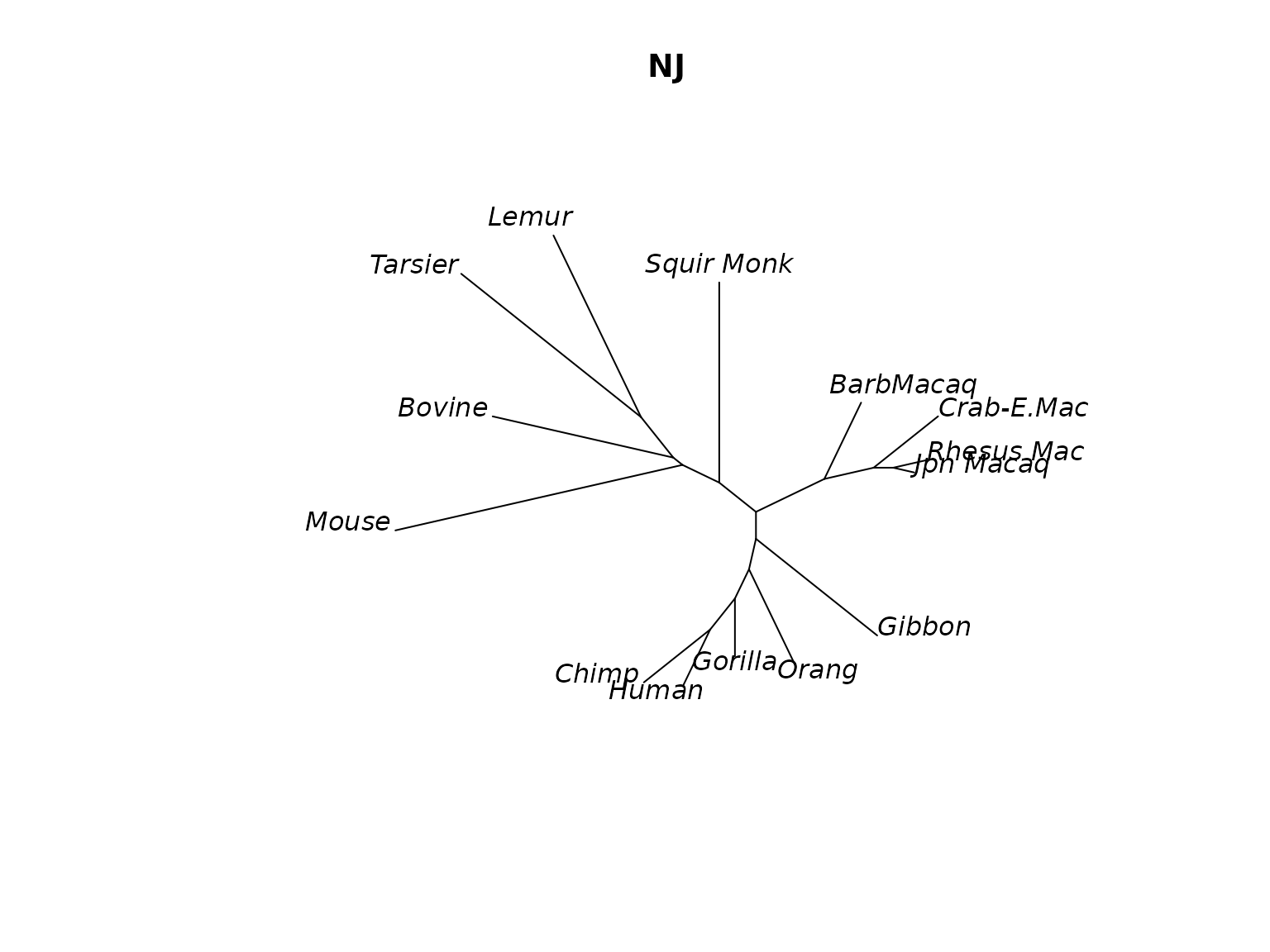
Unrooted NJ tree.
Bootstrap
To run the bootstrap we first need to write a function which computes
a tree from an alignment. So we first need to compute a distance matrix
and afterwards compute the tree. We can then give this function to the
bootstrap.phyDat function.
fun <- function(x) upgma(dist.ml(x))
bs_upgma <- bootstrap.phyDat(primates, fun)With the new syntax of R 4.1 this can be written a bit shorter:
Finally, we can plot the tree with bootstrap values added:
plotBS(treeUPGMA, bs_upgma, main="UPGMA")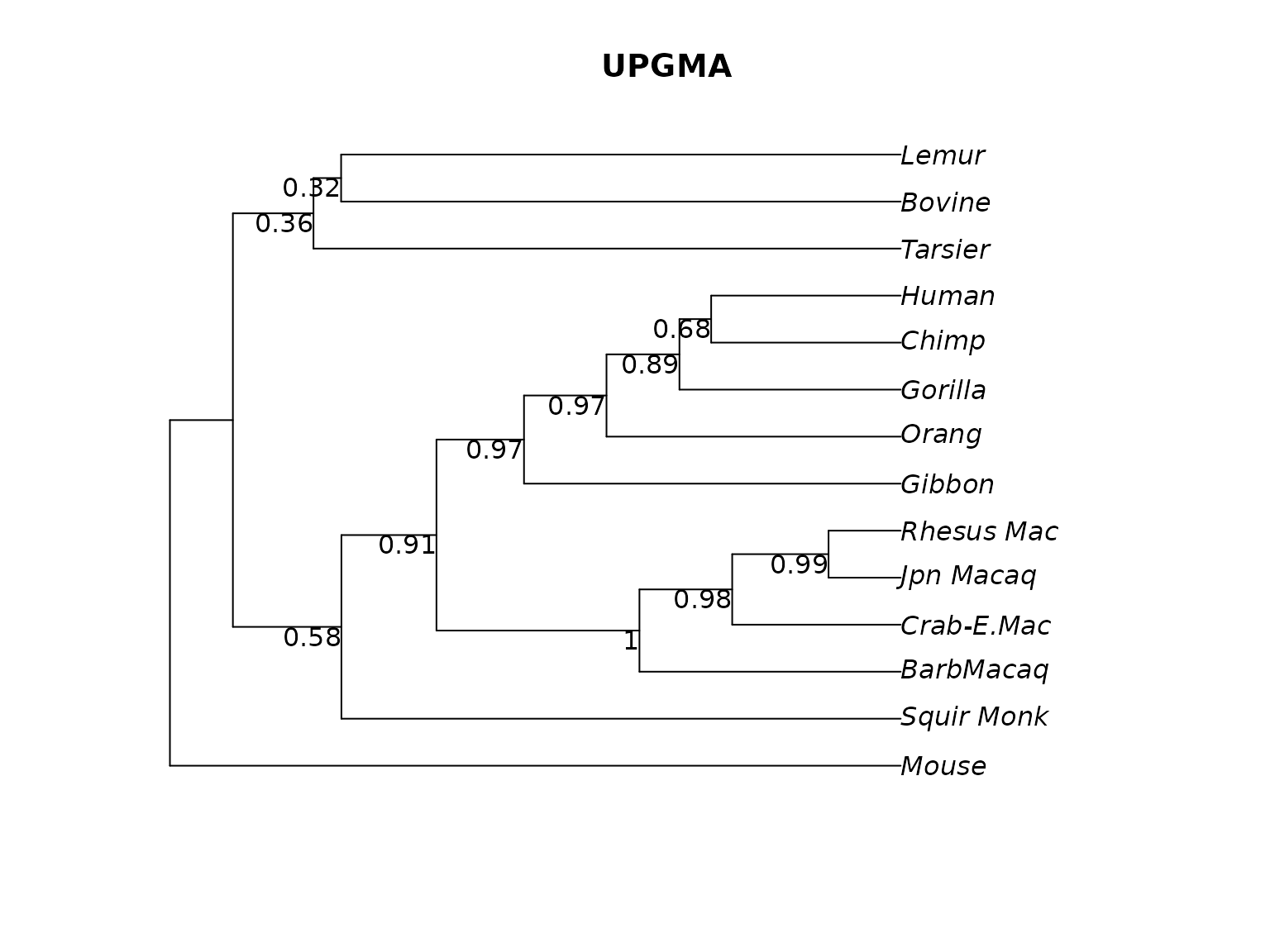
Rooted UPGMA tree.
Distance based methods are very fast and we will use the UPGMA and NJ tree as starting trees for the maximum parsimony and maximum likelihood analyses.
Parsimony
The function parsimony returns the parsimony score, that is the minimum number of changes necessary to describe the data for a given tree. We can compare the parsimony score for the two trees we computed so far:
parsimony(treeUPGMA, primates)## [1] 751
parsimony(treeNJ, primates)## [1] 746The function most users want to use to infer phylogenies with MP
(maximum parsimony) is pratchet, an implementation of the
parsimony ratchet (Nixon 1999). This
allows to escape local optima and find better trees than only performing
NNI / SPR rearrangements.
The current implementation is
- Create a bootstrap data set from the original data set.
- Take the current best tree and perform tree rearrangements on and save bootstrap tree as .
- Use and perform tree rearrangements on the original data set. If this tree has a lower parsimony score than the currently best tree, replace it.
- Iterate 1:3 until either a given number of iteration is reached
(
minit) or no improvements have been recorded for a number of iterations (k).
## [1] 746Here we set the minimum iteration of the parsimony ratchet
(minit) to 100 iterations, the default number for
k is 10. As the ratchet implicitly performs bootstrap
resampling, we already computed some branch support, in our case with at
least 100 bootstrap iterations. The parameter trace=0 tells
the function not write the current status to the console. The function
may return several best trees, but these trees have no branch length
assigned to them yet. Now let’s do this:
treeRatchet <- acctran(treeRatchet, primates)After assigning edge weights, we prune away internal edges of length
tol (default = 1e-08), so our trees may contain
multifurcations.
treeRatchet <- di2multi(treeRatchet)Some trees might have differed only between edges of length 0.
As mentioned above, the parsimony ratchet implicitly performs a bootstrap analysis (step 1). We make use of this and store the trees which where visited. This allows us to add bootstrap support values to the tree.
plotBS(midpoint(treeRatchet), type="phylogram")
add.scale.bar()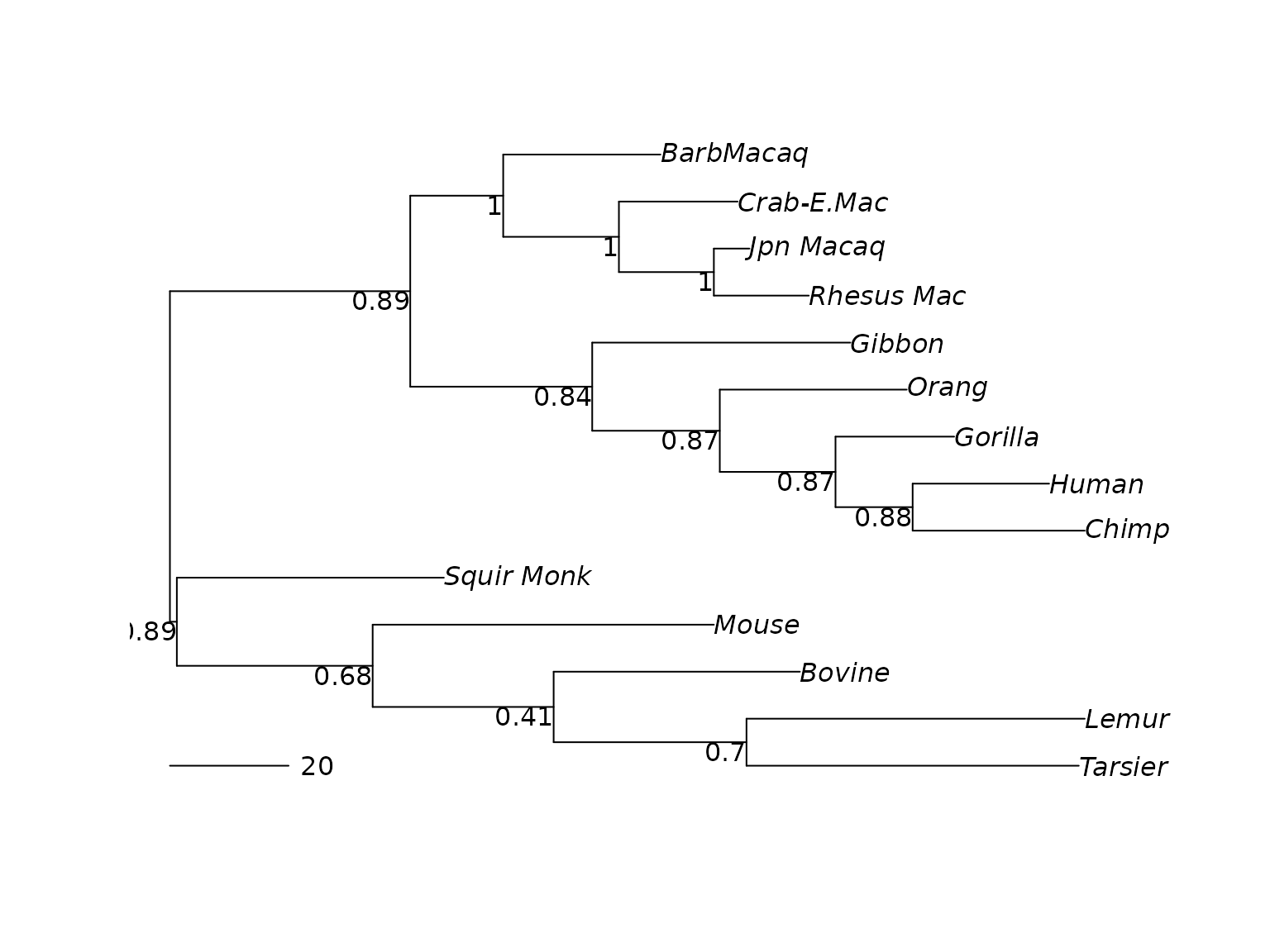
MP phylogeny with bootstrap values.
If treeRatchet is a list of trees, i.e. an object of
class multiPhylo, we can subset the i-th trees with
treeRatchet[[i]].
While in most cases pratchet will be enough to use,
phangorn exports some function which might be useful.
random.addition computes random addition and can be used to
generate starting trees. The function optim.parsimony
performs tree rearrangements to find trees with a lower parsimony score.
The tree rearrangements implemented are nearest-neighbor interchanges
(NNI) and subtree pruning and regrafting (SPR). The latter so far only
works with the fitch algorithm.
treeRA <- random.addition(primates)
treeSPR <- optim.parsimony(treeRA, primates)
parsimony(c(treeRA, treeSPR), primates)## [1] 753 750Branch and bound
For data sets with few species it is also possible to find all most parsimonious trees using a branch and bound algorithm (Hendy and Penny 1982). For data sets with more than 10 taxa this can take a long time and depends strongly on how “tree-like” the data is. And for more than 20-30 taxa this will take almost forever.
(trees <- bab(primates[1:10,], trace=0))## 1 phylogenetic treeMaximum likelihood
The last method we will describe in this vignette is Maximum Likelihood (ML) as introduced by Felsenstein (Felsenstein 1981).
Model selection
Usually, as a first step, we will try to find the best fitting model.
For this we use the function modelTest to compare different
nucleotide or protein models with the AIC, AICc or BIC, similar to
popular programs ModelTest and ProtTest (D.
Posada and Crandall 1998; David Posada 2008; Abascal, Zardoya, and
Posada 2005). By default available nucleotide or amino acid
models are compared.
The Vignette Markov models and transition rate matrices gives further background on those models, how they are estimated and how you can work with them.
mt <- modelTest(primates)It’s also possible to only select some common models:
The results of modelTest is illustrated in following
table:
| Model | df | logLik | AIC | AICw | AICc | AICcw | BIC | rate_model | k | shape | inv | TL | a | c | g | t | a-c | a-g | a-t | c-g | c-t | g-t |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| JC | 25 | -3068.42 | 6186.83 | 0.00 | 6193.15 | 0.00 | 6273.00 | NA | 1 | NA | 0.00 | 4.23 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| JC+I | 26 | -3062.63 | 6177.26 | 0.00 | 6184.10 | 0.00 | 6266.87 | NA | 1 | NA | 0.04 | 4.31 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| JC+G(4) | 26 | -3066.92 | 6185.83 | 0.00 | 6192.68 | 0.00 | 6275.45 | gamma | 4 | 12.21 | 0.00 | 4.34 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| JC+G(4)+I | 27 | -3062.71 | 6179.43 | 0.00 | 6186.84 | 0.00 | 6272.49 | gamma | 4 | 100.00 | 0.04 | 4.32 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| F81 | 28 | -2954.83 | 5965.66 | 0.00 | 5973.66 | 0.00 | 6062.16 | NA | 1 | NA | 0.00 | 4.83 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| F81+I | 29 | -2948.22 | 5954.43 | 0.00 | 5963.05 | 0.00 | 6054.39 | NA | 1 | NA | 0.04 | 4.96 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| F81+G(4) | 29 | -2952.16 | 5962.33 | 0.00 | 5970.94 | 0.00 | 6062.28 | gamma | 4 | 7.62 | 0.00 | 5.10 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| F81+G(4)+I | 30 | -2948.20 | 5956.40 | 0.00 | 5965.65 | 0.00 | 6059.80 | gamma | 4 | 89.93 | 0.04 | 4.99 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 1.00 | 1.00 | 1 | 1.00 | 1 |
| K80 | 26 | -2952.94 | 5957.89 | 0.00 | 5964.73 | 0.00 | 6047.50 | NA | 1 | NA | 0.00 | 4.66 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 3.78 | 1.00 | 1 | 3.78 | 1 |
| K80+I | 27 | -2944.51 | 5943.02 | 0.00 | 5950.43 | 0.00 | 6036.08 | NA | 1 | NA | 0.04 | 4.86 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 3.93 | 1.00 | 1 | 3.93 | 1 |
| K80+G(4) | 27 | -2944.76 | 5943.53 | 0.00 | 5950.94 | 0.00 | 6036.59 | gamma | 4 | 3.79 | 0.00 | 5.47 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 4.40 | 1.00 | 1 | 4.40 | 1 |
| K80+G(4)+I | 28 | -2942.34 | 5940.68 | 0.00 | 5948.68 | 0.00 | 6037.19 | gamma | 4 | 6.79 | 0.03 | 5.32 | 0.25 | 0.25 | 0.25 | 0.25 | 1.00 | 4.29 | 1.00 | 1 | 4.29 | 1 |
| HKY | 29 | -2627.08 | 5312.15 | 0.00 | 5320.77 | 0.00 | 5412.11 | NA | 1 | NA | 0.00 | 20.69 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 27.69 | 1.00 | 1 | 27.69 | 1 |
| HKY+I | 30 | -2623.45 | 5306.90 | 0.00 | 5316.15 | 0.00 | 5410.30 | NA | 1 | NA | 0.02 | 29.29 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 40.31 | 1.00 | 1 | 40.31 | 1 |
| HKY+G(4) | 30 | -2616.16 | 5292.32 | 0.02 | 5301.58 | 0.09 | 5395.72 | gamma | 4 | 2.38 | 0.00 | 40.17 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 48.99 | 1.00 | 1 | 48.99 | 1 |
| HKY+G(4)+I | 31 | -2615.91 | 5293.83 | 0.01 | 5303.75 | 0.03 | 5400.68 | gamma | 4 | 2.36 | 0.00 | 43.45 | 0.37 | 0.40 | 0.04 | 0.18 | 1.00 | 53.78 | 1.00 | 1 | 53.78 | 1 |
| SYM | 30 | -2813.90 | 5687.79 | 0.00 | 5697.05 | 0.00 | 5791.19 | NA | 1 | NA | 0.00 | 4.49 | 0.25 | 0.25 | 0.25 | 0.25 | 14.24 | 10.81 | 6.09 | 0 | 50.05 | 1 |
| SYM+I | 31 | -2811.73 | 5685.46 | 0.00 | 5695.38 | 0.00 | 5792.31 | NA | 1 | NA | 0.02 | 4.53 | 0.25 | 0.25 | 0.25 | 0.25 | 16.68 | 12.94 | 7.32 | 0 | 57.93 | 1 |
| SYM+G(4) | 31 | -2804.68 | 5671.36 | 0.00 | 5681.28 | 0.00 | 5778.20 | gamma | 4 | 3.65 | 0.00 | 5.39 | 0.25 | 0.25 | 0.25 | 0.25 | 28.03 | 19.59 | 9.54 | 0 | 110.09 | 1 |
| SYM+G(4)+I | 32 | -2804.67 | 5673.34 | 0.00 | 5683.95 | 0.00 | 5783.63 | gamma | 4 | 3.71 | 0.00 | 5.38 | 0.25 | 0.25 | 0.25 | 0.25 | 27.99 | 19.58 | 9.54 | 0 | 109.88 | 1 |
| GTR | 33 | -2618.81 | 5303.61 | 0.00 | 5314.94 | 0.00 | 5417.35 | NA | 1 | NA | 0.00 | 21.19 | 0.37 | 0.40 | 0.04 | 0.18 | 0.51 | 25.02 | 0.41 | 0 | 10.77 | 1 |
| GTR+I | 34 | -2613.78 | 5295.55 | 0.00 | 5307.63 | 0.00 | 5412.74 | NA | 1 | NA | 0.02 | 32.05 | 0.37 | 0.40 | 0.04 | 0.18 | 0.57 | 47.70 | 0.50 | 0 | 18.31 | 1 |
| GTR+G(4) | 34 | -2608.77 | 5285.55 | 0.59 | 5297.63 | 0.62 | 5402.74 | gamma | 4 | 2.72 | 0.00 | 39.65 | 0.37 | 0.40 | 0.04 | 0.18 | 1.54 | 147.36 | 1.38 | 0 | 51.89 | 1 |
| GTR+G(4)+I | 35 | -2608.22 | 5286.45 | 0.38 | 5299.31 | 0.27 | 5407.09 | gamma | 4 | 2.95 | 0.01 | 44.92 | 0.37 | 0.40 | 0.04 | 0.18 | 152.81 | 17751.29 | 151.74 | 0 | 5913.43 | 1 |
To speed computations up the thresholds for the optimizations in
modelTest are not as strict as for optim.pml
(shown in the coming vignettes) and no tree rearrangements are
performed, which is the most time consuming part of the optimizing
process. As modelTest computes and optimizes a lot of
models it would be a waste of computer time not to save these results.
The results are saved as call together with the optimized trees in an
environment and the function as.pml evaluates this call to
get a pml object back to use for further optimization or
analysis. This can either be done for a specific model, or for a
specific criterion.
Conducting a ML tree
To simplify the workflow, we can give the result of
modelTest to the function pml_bb and optimize
the parameters taking the best model according to BIC. Ultrafast
bootstrapping (Minh, Nguyen, and Haeseler
2013) is conducted automatically if the default
rearrangements="stochastic" is used. If
rearrangements="NNI" is used, no bootstrapping is
conducted.
fit_mt <- pml_bb(mt)
fit_mt## model: HKY+G(4)
## loglikelihood: -2615.015
## unconstrained loglikelihood: -1230.335
## Total tree length: 43.65846
## (expected number of substituions per site)
## Minimal tree length: 3.314655
## (observed substitutions per site)
## Model of rate heterogeneity: Discrete gamma model
## Number of rate categories: 4
## Shape parameter: 2.274446
## Rate Proportion
## 1 0.3239729 0.25
## 2 0.6813481 0.25
## 3 1.0755525 0.25
## 4 1.9191265 0.25
##
## Rates:
## a <-> c : 1
## a <-> g : 54.35617
## a <-> t : 1
## c <-> g : 1
## c <-> t : 54.35617
## g <-> t : 1
##
## Base frequencies:
## a c g t
## 0.37480751 0.40160148 0.03911303 0.18447798We can also use pml_bb with a defined model to infer a
phylogenetic tree.
fitGTR <- pml_bb(primates, model="GTR+G(4)+I")Bootstrap
If we instead want to conduct standard bootstrapping (Felsenstein 1985; Penny and Hendy 1985), we can
do so with the function bootstrap.pml:
bs <- bootstrap.pml(fit_mt, bs=100, optNni=TRUE)Now we can plot the tree with the bootstrap support values on the
edges and compare the standard bootstrap values to the ultrafast
bootstrap values. With the function plotBS it is not only
possible to plot these two, but also the transfer bootstraps (Lemoine et al. 2018) which are especially
useful for large data sets.
plotBS(midpoint(fit_mt$tree), p = .5, type="p", digits=2, main="Ultrafast bootstrap")
plotBS(midpoint(fit_mt$tree), bs, p = 50, type="p", main="Standard bootstrap")
plotBS(midpoint(fit_mt$tree), bs, p = 50, type="p", digits=0, method = "TBE", main="Transfer bootstrap")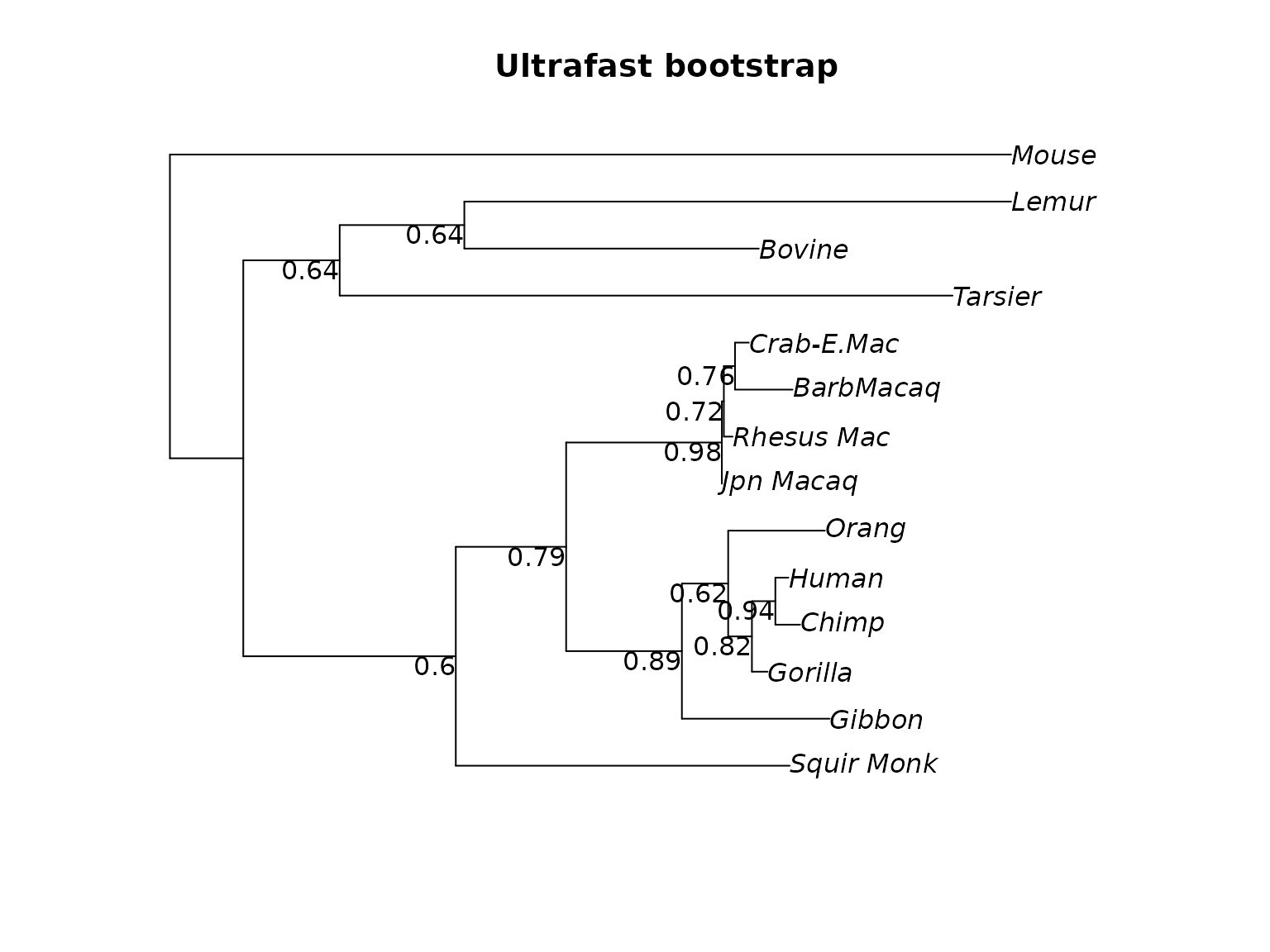
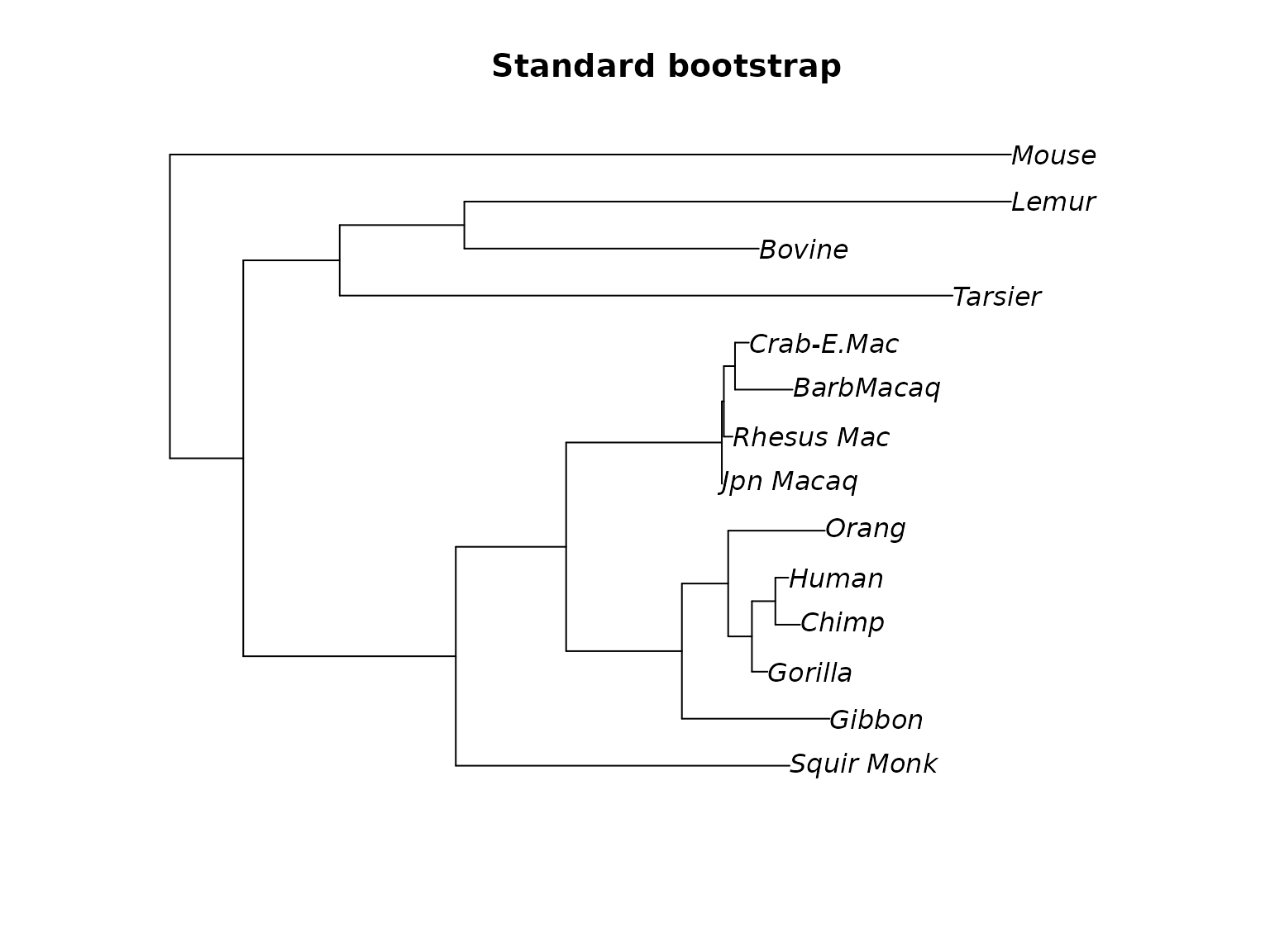
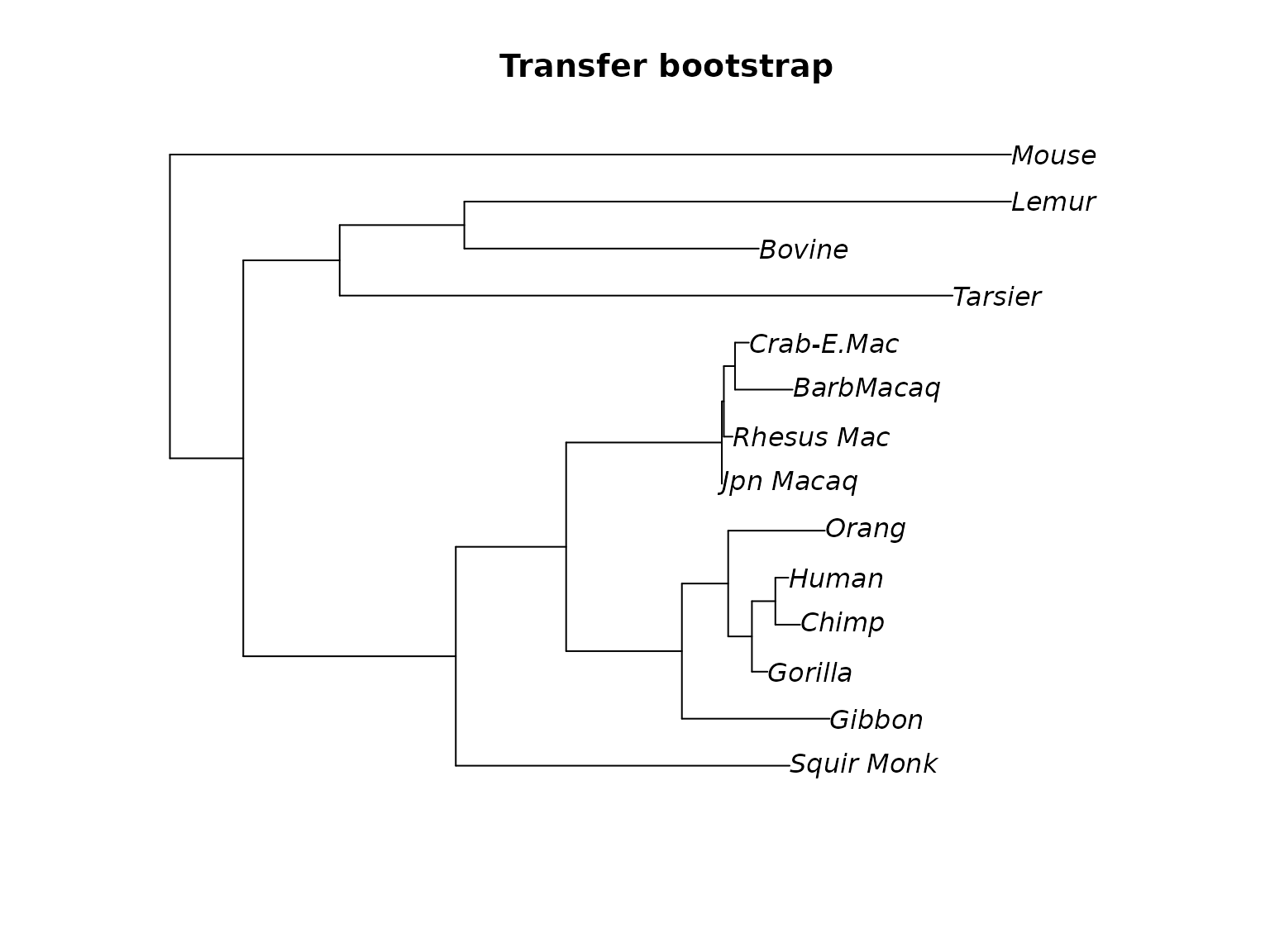
Unrooted tree (midpoint rooted) with ultrafast, standard and transfer bootstrap support values.
If we want to assign the standard or transfer bootstrap values to the
node labels in our tree instead of plotting it (e.g. to export the tree
somewhere else), plotBS gives that option with
type = "n":
# assigning standard bootstrap values to our tree; this is the default method
tree_stdbs <- plotBS(fit_mt$tree, bs, type = "n")
# assigning transfer bootstrap values to our tree
tree_tfbs <- plotBS(fit_mt$tree, bs, type = "n", method = "TBE")It is also possible to look at consensusNet to identify
potential conflict.
cnet <- consensusNet(bs, p=0.2)
plot(cnet, show.edge.label=TRUE)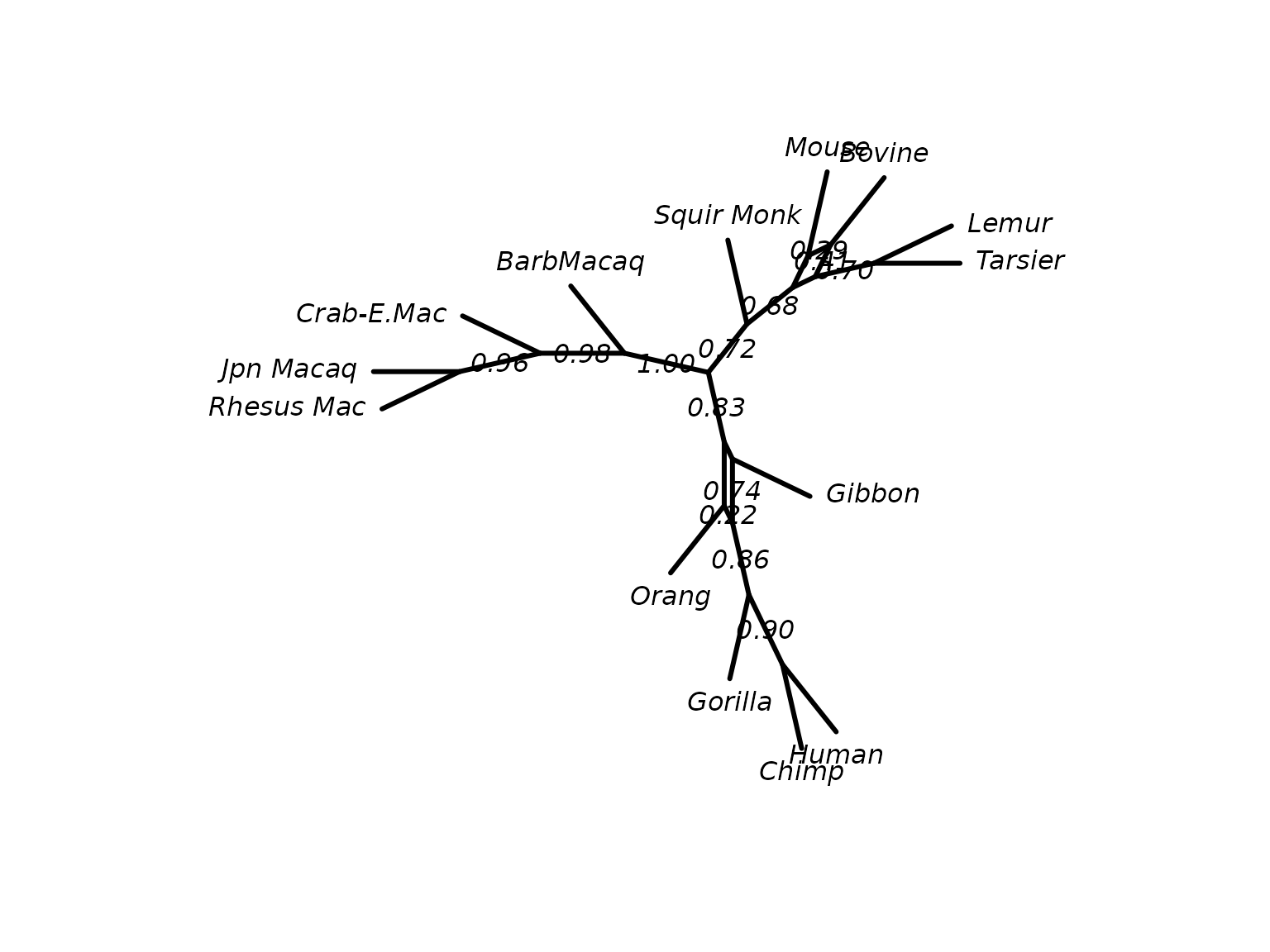
ConsensusNet from the standard bootstrap sample.
Several analyses, e.g.bootstrap and
modelTest, can be computationally demanding, but as
nowadays most computers have several cores, one can distribute the
computations using the parallel package. However, it is only
possible to use this approach if R is running from command line (“X11”),
but not using a GUI (for example “Aqua” on Macs) and unfortunately the
parallel package does not work at all under Windows.
Exporting a tree
Now that we have our tree with bootstrap values, we can easily write it to a file in Newick-format:
# tree with ultrafast bootstrap values
write.tree(fit_mt$tree, "primates.tree")
# tree with standard bootstrap values
write.tree(tree_stdbs, "primates.tree")
# tree with transfer bootstrap values
write.tree(tree_tfbs, "primates.tree")Molecular dating with a strict clock for ultrametric and tipdated phylogenies
When we assume a “molecular clock” phylogenies can be used to infer
divergence times (Zuckerkandl and Pauling
1965). We implemented a strict clock as described in (Felsenstein 2004), p. 266, allowing to infer
ultrametric and tip-dated phylogenies. The function pml_bb
ensures that the tree is ultrametric, or the constraints given by the
tip dates are fulfilled. That differs from the function
optim.pml where th tree supplied to the function has to
fulfill the constraints. In this case for an ultrametric starting tree
we can use an UPGMA or WPGMA tree.
fit_strict <- pml_bb(primates, model="HKY+G(4)", method="ultrametric",
rearrangement="NNI")
plot(fit_strict)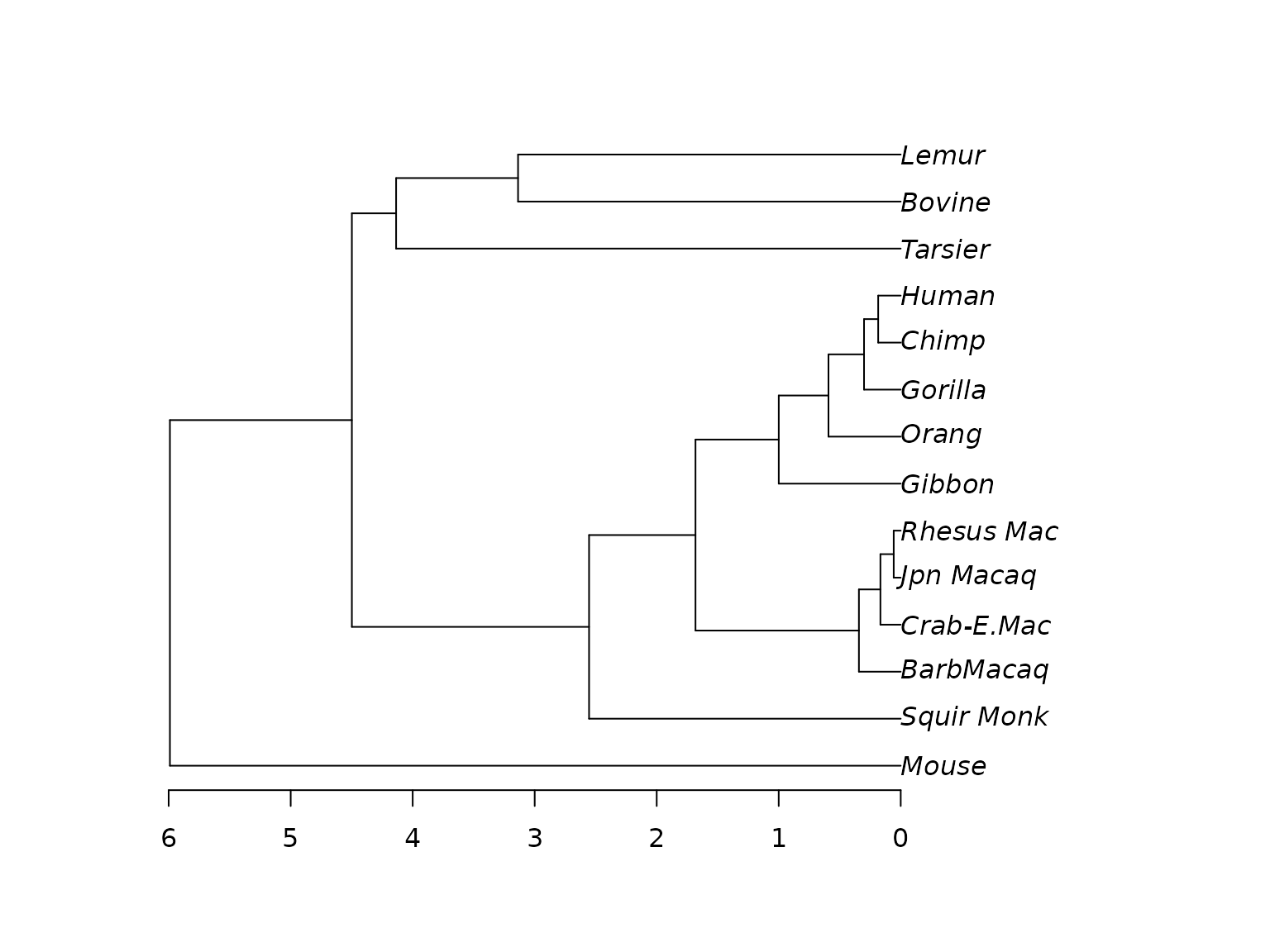
Ultrametric ML phylogeny.
With phangorn we also can estimate tipdated phylogenies. Here we use a H3N2 virus data set from treetime (Sagulenko, Puller, and Neher 2018) as an example. Additionally to the alignment we also need to read in data containing the dates of the tips.
fdir <- system.file("extdata/trees", package = "phangorn")
tmp <- read.csv(file.path(fdir,"H3N2_NA_20.csv"))
H3N2 <- read.phyDat(file.path(fdir,"H3N2_NA_20.fasta"), format="fasta")We first process the sampling dates and create a named vector. The lubridate package (Grolemund and Wickham 2011) comes in very handy dates in case one has to recode dates, e.g. days and months.
## A/Hawaii/02/2013|KF789866|05/28/2013|USA|12_13|H3N2/1-1409
## 2013.405
## A/Boston/DOA2_107/2012|CY148382|11/01/2012|USA|12_13|H3N2/1-1409
## 2012.838
## A/Oregon/15/2009|GQ895004|06/25/2009|USA|08_09|H3N2/1-1409
## 2009.482
## A/Hong_Kong/H090_695_V10/2009|CY115546|07/10/2009|Hong_Kong||H3N2/8-1416
## 2009.523
## A/New_York/182/2000|CY001279|02/18/2000|USA|99_00|H3N2/1-1409
## 2000.134
## A/Canterbury/58/2000|CY009150|09/05/2000|New_Zealand||H3N2/8-1416
## 2000.682Again we use the pml_bb function, which optimizes the
tree given the constraints of the tip.dates vector.
fit_td <- pml_bb(H3N2, model="HKY+I", method="tipdated", tip.dates=dates,
rearrangement="NNI")
fit_td## model: HKY+I
## loglikelihood: -3117.866
## unconstrained loglikelihood: -2883.911
## Total tree length: 0.1321494
## (expected number of substituions per site)
## Minimal tree length: 0.1279318
## (observed substitutions per site)
## Proportion of invariant sites: 0.6865064
##
## Rate: 0.002534975
##
## Rates:
## a <-> c : 1
## a <-> g : 9.866433
## a <-> t : 1
## c <-> g : 1
## c <-> t : 9.866433
## g <-> t : 1
##
## Base frequencies:
## a c g t
## 0.3097759 0.1928617 0.2376819 0.2596805
##
## Rate: 0.002534975While the loglikelihood is lower than for an unrooted tree, we have to keep in mind that rooted trees use less parameters. In unrooted trees we estimate one edge length parameter for each tree, for ultrametric trees we only estimate a parameter for each internal node and for tipdated trees we have one additional parameter for the rate. The rate is here comparable to the slope fo the tip-to-root regression in programs like TempEst (Rambaut et al. 2016).
And at last we plot the tree with a timescale.
plot(fit_td, align.tip.label=TRUE)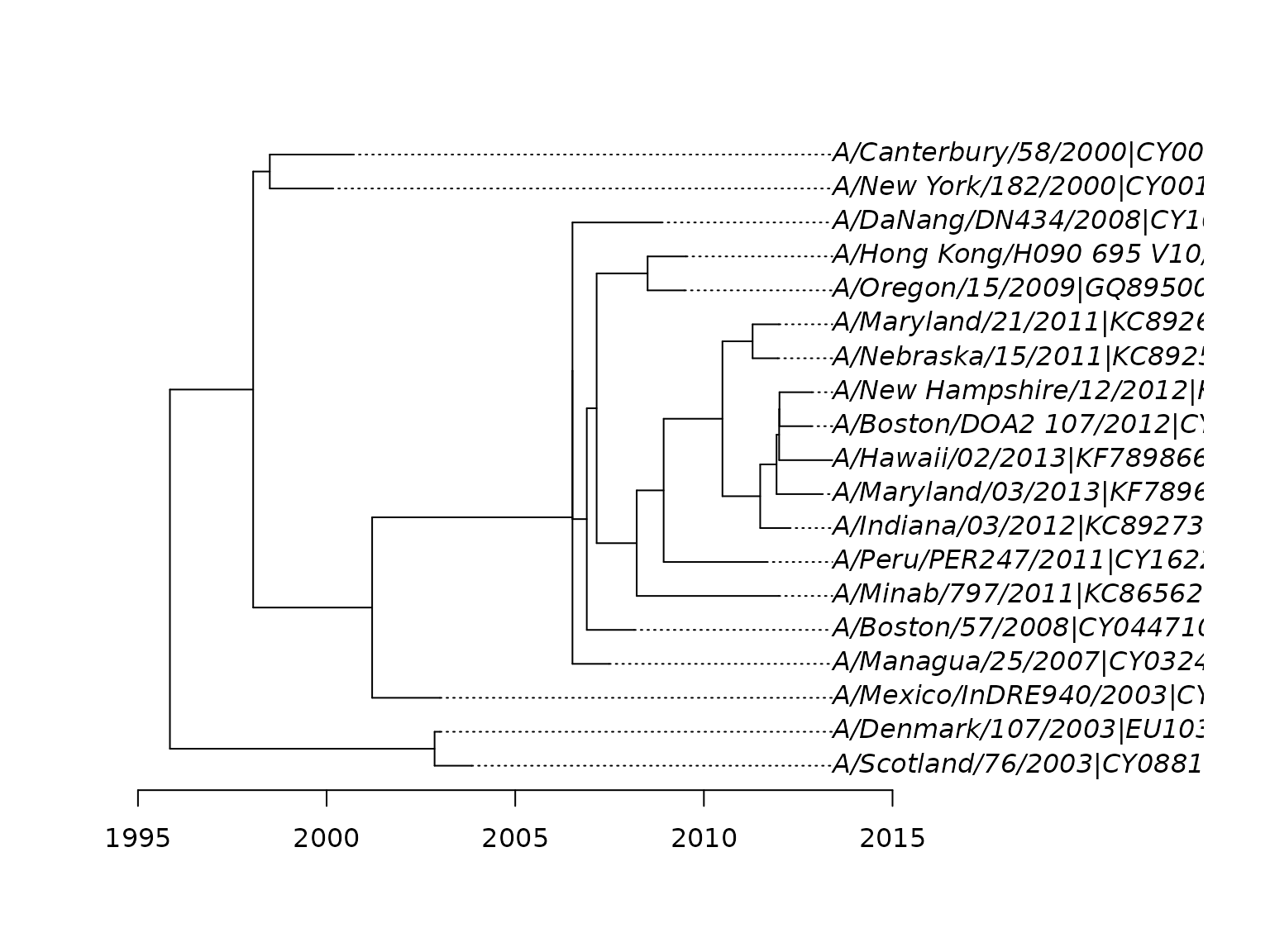
Tip dated ML phylogeny with time scale in years.
Session info
## R version 4.5.2 (2025-10-31)
## Platform: x86_64-pc-linux-gnu
## Running under: Ubuntu 24.04.3 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so; LAPACK version 3.12.0
##
## locale:
## [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
## [4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
## [7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
## [10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
##
## time zone: UTC
## tzcode source: system (glibc)
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] knitr_1.51 future_1.69.0 phangorn_2.12.1.3 ape_5.8-1
##
## loaded via a namespace (and not attached):
## [1] Matrix_1.7-4 future.apply_1.20.2 jsonlite_2.0.0
## [4] compiler_4.5.2 Rcpp_1.1.1 parallel_4.5.2
## [7] jquerylib_0.1.4 globals_0.19.0 systemfonts_1.3.1
## [10] textshaping_1.0.4 yaml_2.3.12 fastmap_1.2.0
## [13] lattice_0.22-7 R6_2.6.1 generics_0.1.4
## [16] igraph_2.2.2 htmlwidgets_1.6.4 backports_1.5.0
## [19] checkmate_2.3.4 desc_1.4.3 osqp_0.6.3.3
## [22] bslib_0.10.0 rlang_1.1.7 fastmatch_1.1-8
## [25] cachem_1.1.0 xfun_0.56 fs_1.6.6
## [28] sass_0.4.10 otel_0.2.0 cli_3.6.5
## [31] pkgdown_2.2.0 magrittr_2.0.4 digest_0.6.39
## [34] grid_4.5.2 lifecycle_1.0.5 nlme_3.1-168
## [37] evaluate_1.0.5 listenv_0.10.0 codetools_0.2-20
## [40] ragg_1.5.0 parallelly_1.46.1 rmarkdown_2.30
## [43] pkgconfig_2.0.3 tools_4.5.2 htmltools_0.5.9